PRIMA DOMANDA
Per poter ricavare la velocità alla fine del piano inclinato dobbiamo utilizzare la conservazione del lavoro considerando come istante finale il momento in cui la sfera tocca il punto più basso del piano.
$L_{tot}=0$
Quindi la somma di energia cinetica ed energia potenziale è uguale a 0
$ΔE_{tot}+ΔU=0$
L'energia cinetica totale è la somma di energia cinetica traslazione e rotazionale della sfera
$ΔE_T+ΔE_R+ΔU=0$
All'inizio la sfera è ferma ed inizia a rotolare per il piano inclinato per effetto della gravità. Quindi la velocità inziale e la velocità angolare iniziale della sfera sono uguali a 0
$ΔE_T=\frac{1}{2}mv_{f}^2-\frac{1}{2}mv_{i}^2=\frac{1}{2}mv_{f}^2$
$ΔE_R=\frac{1}{2}Iω_{f}^2-\frac{1}{2}Iω_{i}^2=\frac{1}{2}Iω_{f}^2$
Per poter rispondere a questa domanda dobbiamo anche considerare un sistema di riferimento dove il punto più basso del piano si trova a $h=0$
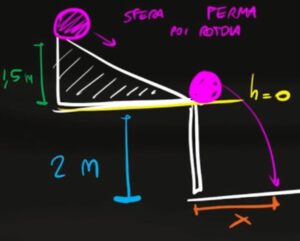
Siccome l'altezza finale è 0, anche l'energia potenziale finale della sfera è 0
$ΔU=mgh_f-mgh_i=-mgh_i$
Mettendo tutto insieme nella formula della conservazione del lavoro otteniamo:
$\frac{1}{2}mv_{f}^2+\frac{1}{2}Iω_{f}^2-mgh_i=0$
La sfera ha momento di inerzia $I=\frac{2}{5}mr^2$
$\frac{1}{2}mv_{f}^2+\frac{1}{5}mr^2ω_{f}^2-mgh_i=0$
Inoltre la sfera si muove sul piano al passo della propria rotazione, quindi la velocità tangenziale e angolare sono legate insieme dalla formula:
$v=ωr$
Da cui possiamo ricavare la velocità angolare finale sostituendo la velocità con la velocità finale
$v_f=ω_fr$
$ω_f=\frac{v_f}{r}$
$ω_{f}^2=\frac{v_{f}^2}{r^2}$
Sostituendo nell'equazione otteniamo:
$\frac{1}{2}mv_{f}^2+\frac{1}{5}mr^2\frac{v_{f}^2}{r^2}-mgh_i=0$
$\frac{1}{2}mv_{f}^2+\frac{1}{5}mv_{f}^2-mgh_i=0$
Sommiamo tra di loro i termini simili
$\frac{7}{10}mv_{f}^2-mgh_i=0$
Per semplificare ancora di più l'equazione dividiamo tutto per $m$
$\frac{7}{10}v_{f}^2-gh_i=0$
Sapendo che l'altezza inziale della sfera è l'altezza del piano inclinato (cioè 1,5 metri) possiamo ricavare la velocità finale risolvendo l'equazione
$v_{f}^2=\frac{10}{7}gh_i$
$v_f=\sqrt{\frac{10}{7}gh_i}=4,58$ $m/s$
SECONDA DOMANDA
Dall'immagine si può capire che il moto della sfera che cade dal piano inclinato è di tipo parabolico, quindi per poter ricavare la velocità finale della sfera che tocca il suolo dobbiamo utilizzare le leggi orarie del moto parabolico
$y=y_i+v_{y_i}t-\frac{1}{2}gt^2$
$v_y=v_{y_i}t-gt$
$x=x_i+v_{x_i}t$
Per ricavare il tempo utilizziamo delle tre l'equazione in cui abbiamo più dati, cioè la prima
$y=y_i+v_{y_i}t-\frac{1}{2}gt^2$
La posizione Y finale della sfera è 0 perché alla fine si trova all'altezza del suolo. La posizione Y inziale invece è di 2 metri dal suolo
$0=2+v_{y_i}t-\frac{1}{2}gt^2$
Inoltre la velocità Y inziale ($v_{y_i}$) è 0 perché nell'istante finale in cui la sfera esce dal piano inclinato la sua velocità è interamente orizzontale
$0=2-\frac{1}{2}gt^2$
$\frac{1}{2}gt^2=2$
Risolvendo l'equazione possiamo ricavare il tempo che impiega a cadere
$t^2=\frac{4}{g}$
$t=\frac{2}{\sqrt{g}}=0,64s$
Ora che abbiamo ricavato il tempo possiamo usare la seconda legge oraria del moto parabolico per poter ricavare la componente Y della velocità finale
$v_y=v_{y_i}-gt$
Come abbiamo detto prima, la velocità inziale della sfera è orizzontale, quindi la velocità inziale verticale è 0
$v_y=-gt=-6,28$ $m/s$
La velocità orizzontale $v_x$ rimane la stessa sia all'inizio che alla fine perché non è soggetta all'accelerazione gravitazionale ed è la stessa velocità calcolata per rispondere alla prima domanda
$v_x=4,58$ $m/s$
Conoscendo le due componenti della velocità possiamo ricavare la velocità della sfera usando il teorema di pitagora
$v=\sqrt{v_{x}^2+v_{y}^2}=7,77$ $m/s$
TERZA DOMANDA
Calcolare quanto lontana va la sfera dal tavolo è l'equivalente di calcolare la posizione X finale della sfera. Per farlo possiamo usare la terza legge oraria del moto parabolico
$x=x_i+v_{x_i}t$
Prima di cadere la sfera si trova sul tavolo, quindi la posizione X iniziale è 0
$x=v_{x_i}t$
La velocità orizzontale inziale l'abbiamo calcolata per rispondere alla prima domanda ed è $v_{x_i}=4,58$ $m/s$ mentre il tempo l'abbiamo calcolato nella seconda domanda ed è $t=0,64s$. Sostituendo i dati otteniamo:
$x=2,93m$
