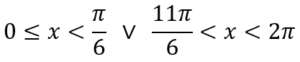Nelle disequazioni goniometriche l'incognita è l'argomento di una funzione trigonometrica. Le principali funzioni sono seno e coseno e per ciascuna funzione ci sono due casi principali
Per il seno dobbiamo considerare i valori sull'asse y, prendiamo per esempio la disequazione
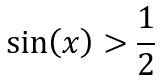
Adesso bisogna applicare l'inverso del seno (arcoseno) al numero indicato
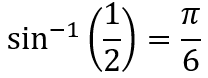
Indichiamo questo risultato con α
Nel caso del seno le intersezioni con l'asse x avvengono con periodicità π
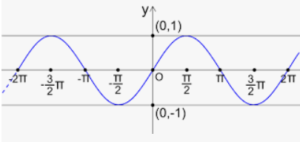
Come si può vedere dal grafico la funzione sin(x) ha valore maggiore di 1/2 per un certo valore di x (π/6) ma il grafico, diminuisce periodicamente quindi x deve essere anche minore di un numero con periodicità 2π.
Come si vede dal grafico i minimi relativi si ripetono con periodicità π quindi il valore minimo (indichiamolo con β) è
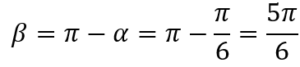
Infine, per risolvere il primo caso di disequazioni goniometriche, basta porre x maggiore di α e minore di β
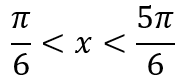
Al risultato applichiamo la periodicità del seno (2kπ)
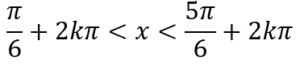
Mentre nel caso in cui il seno fosse stato minore
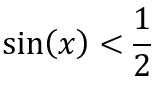
Avremmo dovuto separare le soluzioni in due, una compresa tra 0 e α e un'altra compresa tra β e 2π (compreso lo 0)
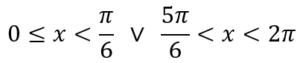
E al risultato aggiungiamo la periodicità
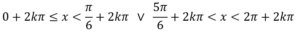
Prendiamo per esempio la seguente disequazione
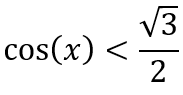
A questo punto, il primo risultato (chiamiamolo α) lo troviamo facendo l'inverso del coseno applicato al numero
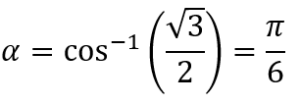
Dal grafico del coseno
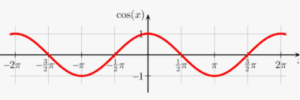
Possiamo vedere che, a partire da 0, il secondo valore per cui $cos(x)<\sqrt{3}/2$ è compreso tra π/6 (primo valore ricavato) e 2π, quindi basta fare la differenza tra i due per trovare il secondo valore.
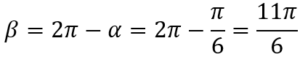
Infine per risolvere l'equazione bisogna trovare i valori tra cui x è compreso, che sono proprio α e β
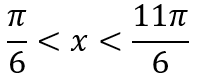
Al risultato aggiungiamo la periodicità del coseno
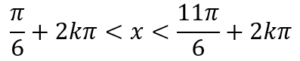
Se invece il coseno fosse stato maggiore
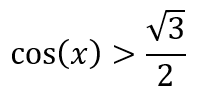
Allora ci sarebbero stati due risultati, uno con x compresa tra 0 e α e un'altra con x compresa tra β e 2π (0 incluso)