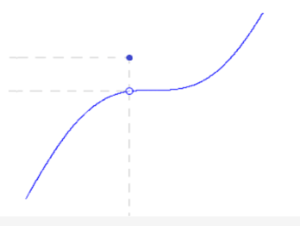
Una funzione è considerata continua se i punti delle funzione sono tutti collegati tra di loro senza alcun distacco, in parole povere una funzione continua è una funzione che si può disegnare tutta senza staccare la matita dal foglio.
Funzione continua:
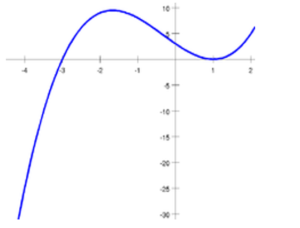
Una funzione discontinua è il contrario delle funzione continua, cioè per disegnarla bisogna, ad un certo punto, staccare la matita dal foglio.
Per le funzioni a tratti si può trovare la specie di discontinuità
(esempio di funzione tratti):

La specie di discontinuità si trova facendo il limite per x che tende al punto in cui avviene il cambio di funzione (nel caso della funzione di sopra il punto di cambio di funzione è 0) di tutte e due le funzioni.
Nel caso del limite di spora bisogna fare:
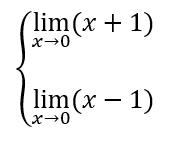
- Se il risultato dei due limiti sono due numeri finiti e diversi allora la discontinuità è di prima specie, detti anche “a salto”.
Esempio di funzione a salto:
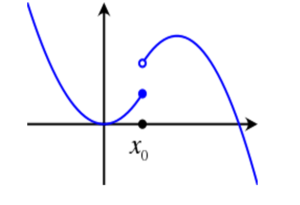
- Se il risultato dei due limiti sono infinito o inesistente allora la discontinuità è di seconda specie.
Esempio di funzione discontinua di seconda specie:
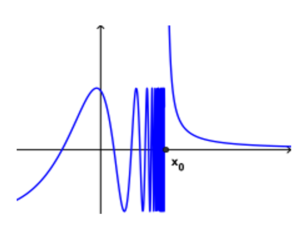
- Se il risultato dei due limiti sono due numeri finiti uguali allora la discontinuità è di terza specie, detta anche “eliminabile” perché si può modificare la discontinuità cambiando l’equazione in un solo punto.
Immagine di una funzione eliminabile: