Mentre gli integrali definiti calcolano aree sottese da funzioni.
Gli integrali indefiniti vengono scritti in questa maniera:

Il dx indica che si vuole calcolare la primitiva della funzione lungo l’asse x.
Gli integrali definiti vengono scritti in questa maniera:
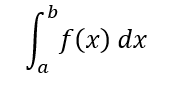
In questo caso il dx indica che si vuole calcolare l’area delimitata dai punti a, b sottesa dalla funzione sull’asse x e, usando la definizione mostrata in precedenza di F(x), possiamo riscrivere l’integrale definito in questo modo:
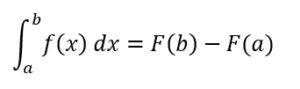
Questo perché le derivate calcolano parti infinitesime di una funzione, un integrale calcola la somma infinita di queste parti infinitesime, cioè l’area (quindi si potrebbe considerare l’integrale indefinito come una formula generale per calcolare l’area di quella determinata funzione ma anche la definizione di primitiva va bene).
Inoltre alla fine di ogni integrale viene addizionata una costante c, questo perché l’integrale trova una funzione che derivata dia la funzione di partenza, ma quando si deriva una costante il risultato è 0 ciò significa che c’è un numero infinito di primitive che possiede una funzione.
