Per poter ricavare la distanza di Alessandro dal centro dell'altalena dobbiamo scrivere l'equilibrio dei momenti. Dato che l'altalena è ferma e non ruota la somma dei momenti di Claudia e Alessandro deve fare 0.
Come si può vedere dall'immagine, il peso di Claudia fa ruotare l'altalena in senso antiorario mentre il peso di Alessandro in senso orario.
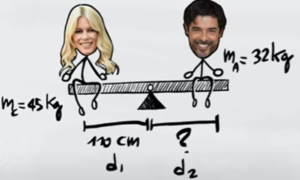
Scrivendo come positivi i momenti antiorari e positivi i momenti orari otteniamo che l'equilibrio dei momenti è:
$M_C-M_A=0$
Usando la formula dei momenti, l'equilibrio diventa
$F_Cd_1sin(θ)-F_Ad_2sin(θ)=0$
Dove θ è l'angolo tra le due forze peso e la distanza tra il centro. In tutti e due i momenti questo angolo è 90°, per cui il seno vale 1
$F_Cd_1-F_Ad_2=0$
Sostituendo le due forze con le forze peso otteniamo
$m_Cgd_1-m_Agd_2=0$
Da questa equazione ricaviamo la distanza di Alessandro dal centro di rotazione $d_2$
$m_Agd_2=m_Cgd_1$
Semplificando in entrambi i lati $g$ otteniamo la distanza $d_2$
$d_2=\frac{m_Cd_1}{m_A}=1,54m$
