Dall'immagine mostrata nel problema
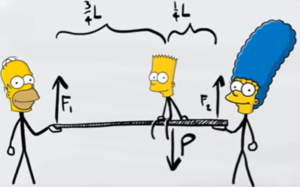
Possiamo vedere che ci sono tre forze in totale: la forza peso, la forza del padre ($F_1$) e la forza della madre ($F_2$). Per far sì che la tavola sia in equilibrio la somma di tutte le forze deve essere uguale a 0 (mettendo come positive le forze verso l'alte e negative quelle verso il basso)
$F_1+F_2-P=0$
$F_1+F_2-mg=0$
EQUILIBRIO DEI MOMENTI
Oltre l'equilibrio delle forze deve esserci anche l'equilibrio dei momenti, perché la tavola né ruota e né si muove. Sulla tavola ci sono due assi di rotazione possibili sui due estremi, scegliamo l'estremo di destra come asse.
La forza $F_1$ e la il peso del bambino $P$ fanno ruotare la tavola in senso orario mentre la forza $F_2$ fa ruotare la tavola in senso antiorario. Scegliendo come positive i momenti antiorari e negativi i momenti orari otteniamo
$M_{F_2}-M_{F_1}-M_{p}=0$
Ogni momenti è data dal prodotto tra forza e distanza dall'asse di rotazione scelto
$F_2d_2-F_1d_1-mgd_p=0$
La distanza tra la forza $F_2$ e l'asse di rotazione è 0 perché abbiamo scelto come asse di rotazione proprio l'estremo destro della tavola che si trova ad una distanza nulla dalla forza $F_2$.
$F_2\cdot 0-F_1d_1-mgd_p=0$
$-F_1d-mgd_p=0$
La distanza tra la forza $F_1$ e l'estremo destro della tavola è la lunghezza stessa della tavola $L$
$-F_1L-mgd_p=0$
Mentre la distanza tra la forza peso e l'estremo destro è riportato nell'immagine a inizio pagina, ed è $L/4$
$-F_1L-mg\frac{L}{4}=0$
Da questa equazione possiamo ricavare la forza $F_1$
$F_1=-mg\frac{L}{4}$
Il meno è presente perché, in questo caso, indica che la forza fa ruotare la tavola in senso orario. ma questo discorso vale per i momenti e non per le forze, per cui la forza $F_1$ va presa positiva dato che punta verso l'alto
$F_1=mg\frac{L}{4}=54N$
EQUILIBRIO DELLE FORZE
Dall'equilibrio delle forze che avevamo scritto precedentemente abbiamo che la somma di tutte le forze è uguale a 0 (prendendo come positive le forze verso l'alto e negative quelle verso il basso)
$F_1+F_2-mg=0$
Sostituendo la forza $F_1$ con quella ricavata nell'equilibrio dei momenti abbiamo
$mg\frac{L}{4}+F_2-mg=0$
Da questa equazione ricaviamo $F_2$
$F_2=mg-mg\frac{L}{4}$
$F_2=mg\frac{3L}{4}=162N$
