PRIMA DOMANDA
Come si può vedere dall'immagine, la forza e la distanza dal centro formano un angolo retto (90°), per cui il seno dell'angolo è 1
$sin(θ)=1$
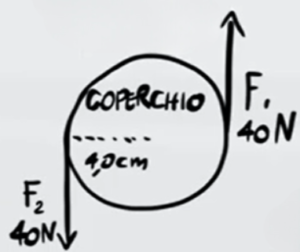
Le due forze hanno stessa intensità e stessa distanza dal centro. Quindi i due momenti associati alle due forze è uguale
$M_1=F_1d$
$M_2=F_2d$
Dove $d$ è la distanza tra la forza e il centro di rotazione, nel caso di un cerchio il centro di rotazione è uguale al centro geometrico, per cui la distanza è il raggio del cerchio
$M_1=F_1r=1,6$ $N\cdot m$
$M_2=F_2r=1,6$ $N\cdot m$
Le due forze sono opposte tra loro, ma fanno ruotare il coperchio nello steso verso (antiorario). Per cui il momento totale è semplicemente la somma dei due momenti
$M_{tot}=M_1+M_2=3,2$ $N\cdot m$
SECONDA DOMANDA
In questo caso il momento necessario per poter aprire il barattolo è lo stesso della prima domanda
$M=3,2$ $N\cdot m$
Dalla formula del momento (dove θ è sempre 90° e $d=0,12m$):
$M=Fdsin(90°)=Fd$
Possiamo ricavare la forza necessaria dalla formula inversa
$F=\frac{M}{d}=27N$
