PRIMA DOMANDA
Nel primo caso il braccio è orizzontale, si forma un angolo di 90° tra la spalla e il trofeo
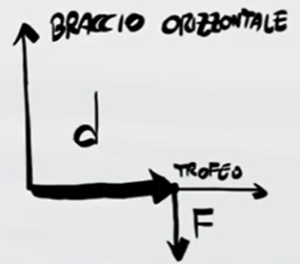
Per ricavare il momento della forza usiamo la formula
$M=Fdsin(θ)$
Dove θ è appunto 90°, il seno di 90° vale uno
$M=Fd$
La forza in questione è la forza esercitata dal braccio sul trofeo, per poter rimanere in equilibrio questa forza deve essere uguale alla forza peso del trofeo. Quindi
$F=mg$
Il momento diventa:
$M=mgd=9,56$ $N\cdot m$
SECONDA DOMANDA
Nel secondo caso il problema è lo stesso, con l'unica differenza che ora l'angolo θ vale 22,5°. Però non è l'angolo che stiamo cercando, l'angolo che a noi interessa è l'angolo tra la forza e la distanza come si può vedere nell'immagine
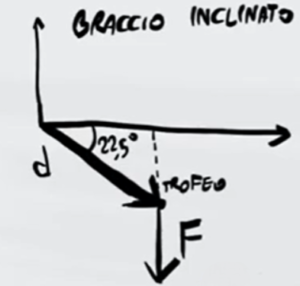
Per poter ricavare quell'angolo dobbiamo prima ricavare l'angolo α all'interno del triangolo rettangolo che si è formato. La somma di tutti gli angoli in un triangolo è 180°, quindi possiamo ricavare α
$22,5+90+α=180$
$α=67,5°$
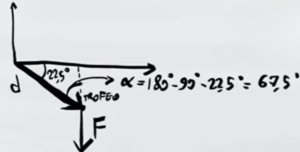
L'angolo che stiamo cercando (chiamiamolo γ) è l'angolo esterno di α. Quindi possiamo ricavarlo sapendo che la loro somma è un angolo piatto, cioè 180°
$γ+67,5°=180°$
$γ=112,5°$
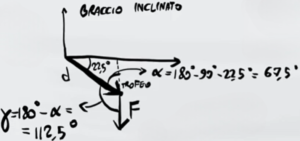
Sostituendo nella formula del momento otteniamo
$M=Fdsin(112,5°)$
Dove la forza è sempre la forza peso del trofeo
$M=mgdsin(112,5°)=8,83$ $N\cdot m$
