Un corpo rigido è un tipo di corpo ideale che non si deforma mai quando è soggetto a forze esterne.
Il momento di una forza indica quanto una forza è in grado di far ruotare un corpo rigido ed è dato dal prodotto vettoriale tra la forza $F$ e il braccio della forza $r$ (cioè la distanza tra il centro di rotazione del corpo e il punto di applicazione della forza)
$\vec{M}=\vec{F}×\vec{r}$
Il prodotto vettoriale indica che il risultato, cioè il momento, è un vettore. Il verso di questo vettore indica la rotazione del corpo. Viene indicato con momento positivo un corpo che ruota in senso antiorario e con verso negativo un corpo che ruota in senso orario.
Per calcolare l'intensità del momento basta aggiungere il seno dell'angolo che si crea tra il braccio della forza e la forza stessa
$M=F\cdot r\cdot sin(α)$
Ad ogni forza agente su un corpo corrisponde un momento. In un sistema in equilibrio la somma di tutti i momenti delle forze è uguale a 0
- Esercizio 1
Durante una premiazione di un torneo di calcio il vincitore tiene in mano un trofeo di massa $m=1,61kg$ ad una distanza dalla spalla di $d=0,605m$. Calcola il momento esercitato dal trofeo sulla spalla nei due casi:
a) Il braccio è orizzontale
b) Il braccio è inclinato di 22,5°
- Esercizio 2
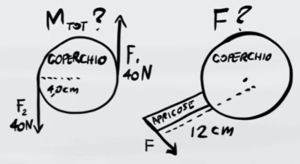
Per aprire un barattolo si applica una coppia di forze con la stessa intensità di $F=40N$. Il coperchio del barattolo è circolare con raggio $r=0,04m$.
a) Quanto vale il momento della forza delle due forze?
b) Se si usa un apribarattolo quanta forza devo applicare ad una distanza di 12 centimetri dal centro per svitare il coperchio?
- Esercizio 3
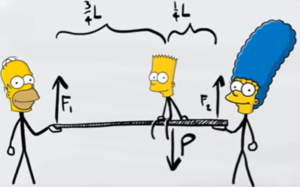
Un bambino di massa $m=22kg$ è seduto su una tavola di legno di lunghezza $L=2m$ sostenuta dai suoi genitori che applicano una forza $F_1$ e $F_2$ come in figura. La forza $F_1$ si trova a $3L/4$ dal bambino mentre la forza $F_2$ si trova a $L/4$ dal bambino.
Calcola l'intensità delle due forze per mantenere l'equilibrio.
- Esercizio 4
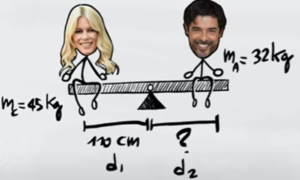
Claudia e Alessandro si trovano su una altalena. Claudia ha una massa $m_C=45kg$ e si trova a 110 centimetri dal centro centro di rotazione dell'altalena. Alessandro ha una massa $m_A=32kg$. A quale distanza dal centro dell'altalena si deve posizionare Alessandro affinché il sistema rimanga in equilibrio?
- Esercizio 5
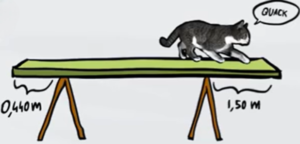
Un gatto di massa cammina lungo una tavola di massa $m=7kg$ e lunga $L=4m$. La tavola è sostenuta da due cavalletti; uno posto a 0,44 metri dall'estremità sinistra della tavola e l'altro a 1,5 metri dall'estremità destra. Quando il gatto raggiunge l'estremità destra, la tavola inizia a sollevarsi
a) Qual è la massa del gatto?
b) Se il gatto ha una massa $m=2,8kg$, a quale distanza dall'estremità destra può arrivare prima che la tavola inizi a ribaltarsi?
- Esercizio 6
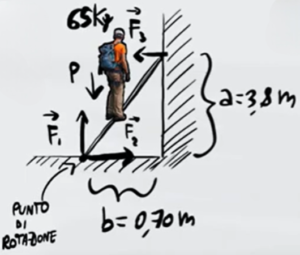
Una persona di massa $m=65kg$ si trova su una scala di massa trascurabile come mostrato in figura. Il pavimento esercita sulla scala una reazione vincolare $F_1$ e una forza di attrito $F_2$. La parete invece è priva di attrito ed esercita una reazione vincolare $F_3$.
Sapendo che l'altezza della scala è $a=3,8m$, la lunghezza della base è $b=0,7m$ e che l'uomo si trova al centro della scala, determina l'intensità di tutte le forze in equilibrio.