Dal secondo principio della dinamica sappiamo che la somma di tutte le forze è uguale al prodotto tra massa e accelerazione del corpo, in questo caso possiamo considerare l'accelerazione del centro di massa.
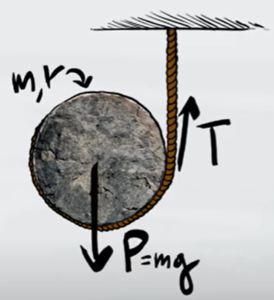
Le forze agenti sul disco sono la forza peso e la tensione.
$mg-T=ma_{CM}$
Questo perché il disco è circolare e la sua massa è distribuita in maniera omogenea, per cui l'accelerazione del centro di massa parte precisamente dal centro del disco proprio come l'accelerazione normale.
MOMENTI
Oltre il secondo principio della dinamica abbiamo anche una legge per i momenti. Infatti la somma di tutti i momenti agenti sul disco è uguale al prodotto tra momento di inerzia e accelerazione angolare (in pratica si tratta del secondo principio della dinamica per le rotazioni)
$M_P+M_T=Iα$
Scriviamo i due momenti come il prodotto tra la forza e la distanza tra il centro di rotazione del disco (cioè il centro geometrico).
$mgd+Td=Iα$
Il peso è una forza che ha come direzione il centro del corpo, per cui la sua distanza dal centro è 0. La distanza tra la tensione del filo e il disco, invece, è il raggio stesso del disco come si può vedere nell'immagine
$Tr=Iα$
L'accelerazione angolare è il rapporto tra l'accelerazione del centro di massa e il raggio del disco
$α=\frac{a_{CM}}{r}$
Il momento di inerzia di un disco è:
$I=\frac{1}{2}mr^2$
Quindi l'equazione dei momenti diventa:
$Tr=\frac{1}{2}mra_{CM}$
Semplificando ad entrambi i membri dell'equazione $r$ otteniamo:
$T=\frac{1}{2}ma_{CM}$
SISTEMA DI EQUAZIONI
Ora abbiamo due equazioni per poter ricavare l'accelerazione del centro di massa e la tensione: il secondo principio della dinamica e l'equazione dei momenti
$mg-T=ma_{CM}$
$T=\frac{1}{2}ma_{CM}$
Dalla seconda equazione abbiamo ricavato la tensione che possiamo sostituire nella prima equazione per poter ricavare l'accelerazione
$mg-\frac{1}{2}ma_{CM}=ma_{CM}$
$mg=ma_{CM}+\frac{1}{2}ma_{CM}$
Semplificando otteniamo:
$mg=\frac{3}{2}ma_{CM}$
$a_{CM}=\frac{2}{3}\cdot \frac{mg}{m}=\frac{2}{3}g$
Dalla formula della tensione che abbiamo utilizzato per ricavare l'accelerazione del centro di massa:
$T=\frac{1}{2}ma_{CM}$
Possiamo ricavare la tensione stessa sostituendo nella formula l'accelerazione del centro di massa ricavata
$T=\frac{1}{2}m\cdot \frac{2}{3}g=\frac{1}{3}mg$
