Il centro di massa indica il punto che corrisponde alla distribuzione nello spazio della massa di uno o più corpi. In pratica il centro di massa indica il punto in cui il peso è bilanciato.
Una volta creato il proprio sistema di riferimento, il punto di distribuzione media della massa (cioè il centro di massa) si calcola considerando le coordinate di ogni singolo corpo e la propria massa
$X_{CM}=\frac{m_1x_1+m_2x_2+...}{m_1+m_2+...}$
Dove $m_1,m_2...$ sono le masse dei vari corpi mentre $x_1,x_2...$ sono le corrispettive coordinate nel nostro sistema di riferimento. Per poter individuare il punto nello spazio dobbiamo trovare anche la coordinata Y del centro di massa
$Y_{CM}=\frac{m_1y_1+m_2y_2+...}{m_1+m_2+...}$
Il centro di massa non serve solo a trovare la distribuzione media della massa nello spazio ma può essere utile per ricavare anche la distribuzione della velocità e l'accelerazione dei vari corpi
$v_{CM}=\frac{m_1v_1+m_2v_2+...}{m_1+m_2+...}$
$a_{CM}=\frac{m_1a_1+m_2a_2+...}{m_1+m_2}$
Quest'ultime due formule sono utili quando si considerano più corpi in movimento come un unico corpo con velocità e accelerazione date dal centro di massa
- Esercizio 1
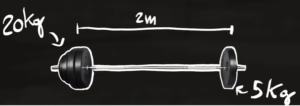
In palestra una persona monta male un bilanciere lungo 2 metri e di massa trascurabile mettendo da un lato un peso di 20 chilogrammi e dall'altro lato un peso da 5 chilogrammi. Qual è il centro di massa del bilanciere?
- Esercizio 2
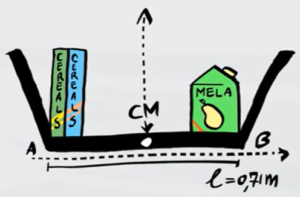
Sei al supermercato e stai reggendo un cestino lungo $l=0,71m$ contenente due scatoloni di cereali di massa uguale $m=0,56kg$ posti sull'estremità sinistra del cestino. A quale distanza dall'estremità sinistra dovresti mettere un cartone di succo di frutta di massa $m=1,8kg$ affinché il centro di massa sia precisamente al centro del cestino?
- Esercizio 3
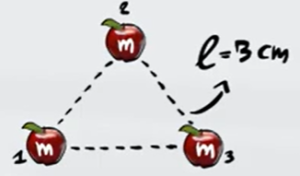
Calcola le coordinate del centro di massa di tre corpi di massa uguale $m$ posti ai vertici di un triangolo equilatero di lunghezza $l=3cm$.
- Esercizio 4 (momento di inerzia)
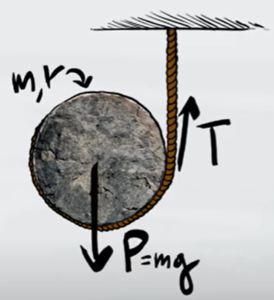
Un disco di massa $m$ e di raggio $r$ scende srotolando un filo che non slitta rispetto al bordo del disco. Determina l'accelerazione del centro di massa e la tensione del filo
- Esercizio 5 (quantità di moto)
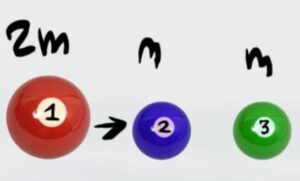
Tre palle da biliardo di massa $m_1=2m$, $m_2=m$ e $m_3=m$ sono allineate ferme su un piano senza attrito. La prima palla viene lanciata contro la seconda con velocità inziale $v_{1i}=9$ $m/s$ mettendo in moto la seconda palla che mette in moto la terza. Qual è la velocità finale della seconda e della terza palla $v_{2f}=?$, $v_{3f}=?$
- Esercizio 6 (quantità di moto)
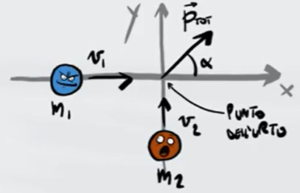
Due palline di massa $m_1$ e $m_2$ si muovono perpendicolarmente tra loro e finiscono per scontrarsi in un urto anelastico. Dopo lo scontro le due palline formano un angolo α tra di loro. Ricava l'equazione per poter calcolare la velocità del centro di massa e l'angolo α.
- Esercizio 7 (quantità di moto)
Un uomo di massa $m_U=60kg$ viaggia su un carrello di massa $m_C=30kg$ con una velocità del centro di massa pari a $v_{CM}=2$ $m/s$. Ad un certo punto l'uomo salta dal carrello in direzione opposta al moto con velocità rispetto al suolo $v_U=1$ $m/s$.
a) Qual è la velocità del centro di massa del sistema uomo-carrello prima e dopo il salto?
b) Qual è la velocità finale del carrello dopo il salto?
c) Calcola la velocità del centro di massa dopo che l'uomo ha toccato il terreno fermandosi