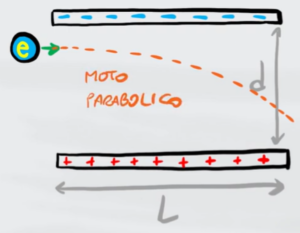
L'elettrone, man mano che si muove, va verso la piastra carica positiva che si trova in basso creando un moto che sul piano può essere rappresentato come un moto parabolico
PRIMA DOMANDA
Innanzitutto scriviamoci le due equazioni del moto parabolico per le coordinate X e Y della particella
$y=y_0+v_{0y}t+\frac{1}{2}at^2$
$x=x_0+v_{0x}t$
Scegliamo come sistema di riferimento il punto da cui parte l'elettrone per cui $x_0=0$ e $y_0=0$
$y=v_{0y}t+\frac{1}{2}at^2$
$x=v_{0x}t$
Dall'immagine sopra possiamo vedere che l'angolo di inclinazione della parabola inziale è 0°, quindi la componente Y della velocità iniziale è 0 mentre la componente X della velocità iniziale diventa semplicemente la velocità totale inziale (che abbiamo già dai dati)
$y=\frac{1}{2}at^2$
$x=v_{0}t$
Dobbiamo ricavare il tempo per poter trovare l'incognita $X$. Per farlo usiamo l'equazione della $Y$, per prima cosa calcoliamo l'accelerazione utilizzando il secondo principio della dinamica
$a=\frac{F}{m}$
Dove $m$ è la massa dell'elettrone e $F$ è la forza totale data dal prodotto tra il campo elettrico totale e la carica dell'elettrone. Quindi la forza totale è:
$F=|q|E$
Sostituiamo il campo elettrico totale con la formula del campo elettrico tra due piastre cariche
$F=\frac{|q|σ}{ε_0}$
Sostituiamo all'interno della formula dell'accelerazione
$a=\frac{|q|σ}{mε_0}$
Sostituiamo all'interno del sistema di equazioni del moto e otteniamo
$y=\frac{|q|σ}{2mε_0}t^2$
$x=v_{0}t$
La posizione $Y$ finale dell'elettrone è $d$ perché alla fine del moto, quando arriva al punto più basso, si trova ad un'altezza $d$ come si può vedere dall'immagine sopra
$d=\frac{|q|σ}{2mε_0}t^2$
$x=v_{0}t$
Dalla prima equazione possiamo ricavare il tempo dividendo entrambi i membri per tutta l'espressione che moltiplica $t$
$t^2=\frac{2mε_0d}{|q|σ}$
Applichiamo ad entrambi i membri la radice quadrata per ottenere il tempo che impiega l'elettrone per arrivare alla fine
$t=\sqrt{\frac{2mε_0d}{|q|σ}}$
Ora che abbiamo il tempo possiamo sostituirlo nella seconda equazione per ricavare la posizione $X$ finale dell'elettrone
$x=v_0t=v_0\sqrt{\frac{2mε_0d}{|q|σ}}$
Sostituendo i dati otteniamo
$x=8,98\cdot 10^{-5}m$
Questo valore è molto più piccolo della lunghezza delle piastre, questo significa che l'elettrone non riesce ad uscire dalle due piastre perché arriva a "sbattere" prima contro la piastra positiva che sta in basso.
SECONDA DOMANDA
Dato che l'elettrone tocca le piastre, dobbiamo calcolare la velocità al tocco, per farlo basta utilizzare il teorema di Pitagora conoscendo il valore della velocità lungo l'asse X (che è sempre uguale alla velocità iniziale ed è $v_x=4\cdot 10^3$ $m/s$). Per quanto riguarda la velocità lungo l'asse Y possiamo ricavarla utilizzando le leggi del moto accelerato
$v_y=v_{0y}+at$
La velocità iniziale lungo l'asse Y è 0 mentre l'accelerazione e il tempo li abbiamo calcolati per rispondere alla domanda 1
$v_y=at$
Applicando il teorema di Pitagora otteniamo la velocità finale totale
$v=\sqrt{v_{x}^2+v_{y}^2}=\sqrt{v_{x}^2+(at)^2}$
Sostituendo i dati otteniamo:
$v=8,91\cdot 10^5$ $m/s$
