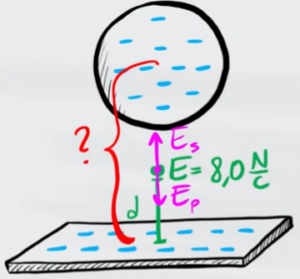
Il punto che stiamo considerando si trova tra la sfera e la piastra, quindi il campo elettrico totale nel punto è dato dalla somma dei campi elettrici della sfera e della piastra
$E=E_{s}+E_{p}$
La sfera e la piastra hanno entrambi carica negativa e siccome si respingono tra loro hanno di conseguenza campi elettrici opposti
Quindi la somma algebrica dei due campi elettrici diventa:
$E=|E_{s}-E_{p}|$
Possiamo togliere il valore assoluto aggiungendo ad entrambi i membri un $±$ in modo da ottenere due risultati per la nostra incognita
$±E=E_{s}-E_{p}$
Ora calcoliamo il campo elettrico dei due oggetti nel punto. Per quanto riguarda la piastra carica, il suo campo elettrico nel punto è:
$E_p=\frac{|σ|}{2ε_0}$
Il campo elettrico della sfera, invece, dipende dalla distanza del punto dal centro della sfera. Come possiamo vedere dall'immagine questa distanza è la differenza tra la distanza del centro della sfera dalla piastra e la distanza $d$
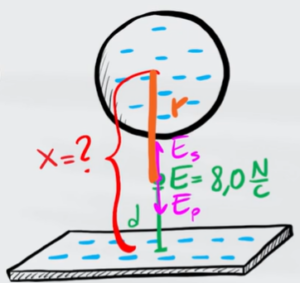
$r=x-d$
Dove $r$ è la distanza tra il centro della sfera e il punto mentre $x$ è la distanza totale tra la sfera e la piastra. Quindi il campo elettrico della sfera diventa:
$E_S=\frac{K|Q_S|}{r^2}=\frac{K|Q_S|}{(x-d)^2}$
Quindi il campo elettrico totale diventa:
$±E=\frac{K|Q_S|}{(x-d)^2}-\frac{|σ|}{2ε_0}$
Isoliamo $x$
$\frac{K|Q_S|}{(x-d)^2}=±E+\frac{|σ|}{2ε_0}$
Moltiplichiamo entrambi i membri per $(x-d)^2$
$K|Q_S|=(±E+\frac{|σ|}{2ε_0})(x-d)^2$
Dividiamo per tutta l'espressione che moltiplica $(x-d)^2$
$(x-d)^2=\frac{K|Q_S|}{±E+\frac{|σ|}{2ε_0}}$
Applichiamo ad entrambi i membri la radice quadrata e spostiamo $d$ dall'altro lato dell'equazione per ricavare $x$
$x=d+\sqrt{\frac{K|Q_S|}{±E+\frac{|σ|}{2ε_0}}}$
Da questa equazione otteniamo due risultati per la distanza $x$: uno con $+E$ e l'altro si ottiene con $-E$. Svolgendo i calcoli otteniamo:
$x_1=0,162m=16,2$ $cm$
$x_2=0,167m=16,7$ $cm$
