La matrice identità è rappresentata dalla seguente matrice(il numero di righe e di colonne indica il numero di dimensioni):
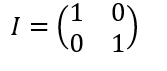
La matrice identità indica una trasformazione lineare in cui asse x e y rimangono invariati, questo perché l’asse x e l’asse y si possono scrivere come vettori:
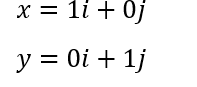
Quindi, scrivendo x e y come matrici, otteniamo:
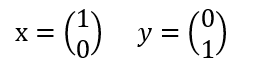
Assemblandoli insieme otteniamo la matrice identità.
Se vogliamo rappresentare una trasformazione lineare dobbiamo sapere le equazioni che descrivono i vettori x e y del sistema di assi cartesiano.
Se, per esempio, consideriamo una trasformazione lineare tale che l’asse x e y vengano rappresentati da questi due vettori:
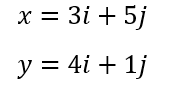
Usando la tecnica mostrata precedentemente ricaviamo la trasformazione lineare A:
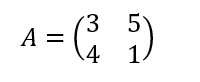
Immaginiamo di disegnare la retta bisettrice sul sistema di assi cartesiani normali, è definito autovettore un vettore che, in seguito alla trasformazione, continua ad avere lo stesso verso della bisettrice.
Gli autovalori sono dei coefficienti che indicano la diminuzione o l’aumento dell’intensità dell’autovettore in seguito alla trasformazione lineare tramite questa equazione:
![]()
In cui v è l’autovettore, l’autovalore e A la matrice di trasformazione.
