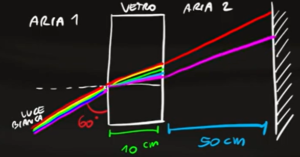
La luce bianca è la somma di tutti i colori e quando entra in contatto con il vetro viene scomposta nei vari colori. Il colore con la lunghezza d'onda più grande è il rosso mentre il colore con la lunghezza d'onda più piccola è il viola. Siccome questi due colori hanno lunghezze d'onda diverse verranno rifratti in due punti diversi dello schermo.
Infatti la richiesta del problema è quella di trovare la larghezza della banda luminosa che si crea sullo schermo, cioè dobbiamo calcolare lo spazio che si crea tra i due estremi della banda (viola e rosso)
Per poter calcolare lo spessore dello banda dobbiamo calcolare le altezze raggiunte dai colori viola e rosso sullo schermo e fare la differenza
ALTEZZA RAGGIUNTA DAL COLORE VIOLA
Consideriamo i due triangoli rettangoli che si sono formati tra la luce e il vetro e tra la luce e lo schermo
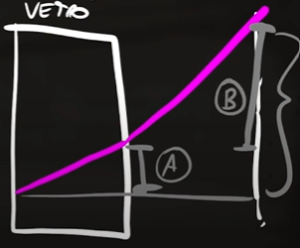
Dove A e B sono le altezze dei due triangoli rettangoli di base $10$ $cm$ e $50$ $cm$. Consideriamo ora il primo triangolo formato all'interno del vetro. Questo triangolo ha un angolo alla base che è dato dalla rifrazione della luce viola nell'aria
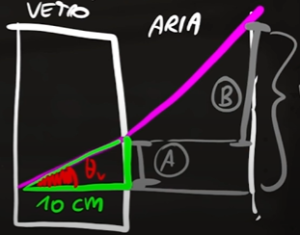
Per ricavare l'angolo $θ_v$ basta utilizzare la formula della rifrazione considerando l'indice di rifrazione del vetro per la luce viola ($n_v=1,7$)
$n_1sin(θ_1)=n_vsin(θ_v)$
L'angolo di rifrazione della luce quando entra nel vetro non è 60° come mostrato nell'immagine del problema, ma è l'angolo formato con il piano, cioè 30°. Da questa equazione possiamo ricavare l'angolo della luce viola all'interno del vetro
$sin(θ_v)=\frac{n_1sin(θ_1)}{n_v}$
Per ricavare il valore dell'angolo basta applicare la funzione inversa del seno
$θ_v=arcsin(\frac{n_1sin(θ_1)}{n_v})=17,10°$
Conoscendo la base e l'angolo adiacente alla base del primo triangolo possiamo ricavare la sua altezza $A$ tramite le formule trigonometriche
$A=10cm\cdot tan(θ_v)=3,08$ $cm$
Ora dobbiamo considerare il triangolo rettangolo che si crea tra la luce viola e lo schermo di base $50$ $cm$
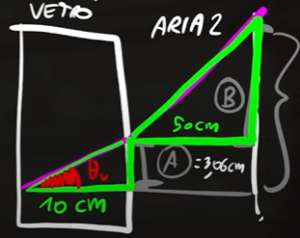
Questa volta la luce ritorno di nuovo nell'aria come all'inizio, quindi l'angolo di rifrazione alla base del triangolo è lo stesso che aveva prima (30°). Conoscendo l'angolo e la base del triangolo possiamo ricavare l'altezza con lo stesso procedimento di prima
$B=50cm\cdot tan(30°)=28,9$ $cm$
Ora che abbiamo le altezze dei due triangoli possiamo ricavare l'altezza della banda viola facendo la somma di questi due
$y_{viola}=A+B=31,98$ $cm$
ALTEZZA RAGGIUNTA DAL COLORE ROSSO
Per il colore rosso il procedimento è lo stesso. Calcoliamo l'angolo di rifrazione della luce che entra nel vetro considerando l'indice di rifrazione del vetro per la luce rossa
$n_1sin(30°)=n_rsin(θ_r)$
$sin(θ_r)=\frac{n_1sin(30°)}{n_r}$
Applichiamo la formula inversa del seno per ricavare l'angolo
$θ_r=arcsin(\frac{n_1sin(30°)}{n_r})=17,31°$
Ora che abbiamo il seno dell'angolo calcoliamo l'altezza del primo triangolo rettangolo (facendo sempre riferimento ai disegni di prima)
$A=10cm\cdot tan(17,31°)=3,12cm$
Adesso calcoliamo l'altezza del secondo triangolo rettangolo sapendo che la base è $b=50$ $cm$ e l'angolo adiacente alla base è lo stesso di quello che aveva la luce nell'aria (30°) dato che si trova nuovamente nell'aria dopo essere uscita dal vetro
$B=50cm\cdot tan(30°)=28,87cm$
Infine sommiamo le due altezze per trovare l'altezza totale della banda rossa
$y_{rosso}=A+B=31,99cm$
RISULTATO
Come abbiamo detto prima lo spessore della banda luminosa sullo schermo è dato dalla differenza tra i due estremi della banda: la luce rossa e la luce viola. Svolgendo questa differenza otteniamo:
$y=y_{rosso}-y_{viola}=31,99cm-31,98cm$
$y=0,01$ $cm$
