I corpi possiedono un energia cinetica data dalla formula generale:
$E=\frac{1}{2}mv^2$
Questa energia è detta energia cinetica traslazionale e corrisponde al lavoro compiuto dal movimento del corpo stesso.
Questa formula però vale solo per i movimenti semplici e non tiene conto delle rotazioni, ma un corpo può compiere lavoro anche stando fermo in un punto a ruotare su sé stesso. Per questo motivo bisogna considerare anche l'energia cinetica rotazionale di un corpo
$E_R=\frac{1}{2}Iω^2$
Dove il momento di inerzia e la velocità angolare corrispondono alla massa e alla velocità lineare in dinamica.
Quindi l'energia cinetica totale di un corpo in movimento rotatorio in un certo istante di tempo è la somma di queste due
$E_{tot}=\frac{1}{2}mv^2+\frac{1}{2}Iω^2$
Quindi il lavoro totale compiuto dal corpo sarà la somma dell'energia cinetica totale ed eventuali energie potenziali
$L_{tot}=ΔE_{tot}+ΔU$
- Esercizio 1
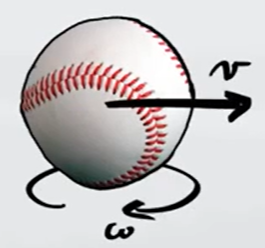
Una persona lancia una palla da baseball di massa $m=0,15kg$ e raggio $r=3,7cm$. Ad un certo punto la pallina raggiunge una velocità lineare di $v=48$ $m/s$ e una velocità angolare $ω=42$ $rad/s$.
a) Qual è l'energia cinetica traslazionale della palla?
b) Qual è l'energia cinetica rotazionale della palla?
- Esercizio 2
Un disco di massa $m=12g$ e raggio $r=6cm$ ruota attorno a sé stesso con velocità angolare $ω=34$ $rad/s$. Qual è la velocità angolare necessaria per far raddoppiare l'energia cinetica rotazionale del disco?

- Esercizio 3 (energia + momento angolare)
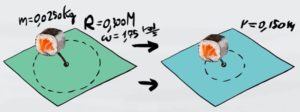
Un blocco di massa $m=0,025kg$ si muove su una superfice orizzontale priva di attrito ed è attaccato alla superfice tramite un filo privo di massa. Inizialmente il blocco ruota ad una distanza dal centro di $R=0,300m$ con una velocità angolare $ω_1=1,75$ $rad/s$.
Successivamente la lunghezza del filo viene ridotta e il filo inizia a ruotare a $r=0,150m$ dal centro.
a) Il momento angolare si conserva?
b) Qual è la velocità angolare del blocco quando il filo viene ridotto?
c) Calcola la variazione di energia cinetica nel blocco
d) Qual è il lavoro totale compiuto dal blocco?
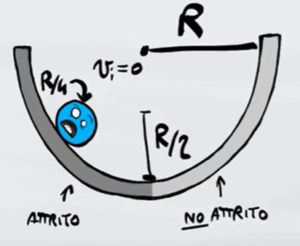
- Esercizio 4 (centro di massa)
Un cilindro di raggio $R/4$ ruota senza strisciare dentro un semi-tubo di raggio $R$. Nella parte sinistra del tubo è presente l'attrito mentre nella parte destra no. Se all'istante inziale il cilindro è fermo a sinistra e il centro di massa è all'altezza $R/2$ calcola:
a) La velocità angolare nel punto più alto raggiunto.
b) L'altezza finale a cui arriva il cilindro nel lato destro
- Esercizio 5 (piano inclinato)
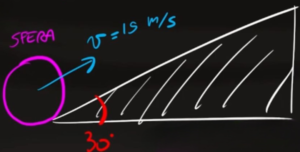
Una sfera di raggio $r=0,10m$ viene lanciata su un piano inclinato di 30° con velocità inziale $v_i=15$ $m/s$. A quale altezza sul piano arriva prima di fermarsi?
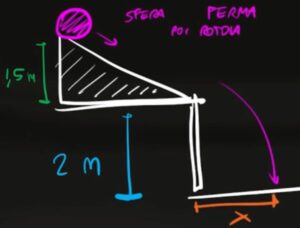
- Esercizio 6 (piano inclinato + moto parabolico)
Una sfera di massa $m=6kg$ e raggio $r=0,5m$ scende da un piano inclinato alto 1,5 metri. Il piano inclinato si trova sopra un tavolo alto 2 metri e dopo che la sfera è scesa dal piano inclinato salta giù dal tavolo.
a) Qual è la velocità della sfera quando arriva alla fine del piano inclinato?
b) Qual è la sua velocità quando tocca terra dopo essere caduta dal tavolo?
c) A che distanza dal tavolo cade la sfera?