Dopo l'urto si crea un angolo α tra le due palline come mostrato in figura
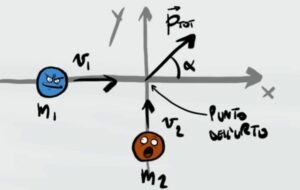
Quindi possiamo scomporre la quantità di moto totale nelle sue due componenti.
$p_{tot_xf}=(m_1+m_2)v_{tot}cos(α)$
$p_{tot_yf}=(m_1+m_2)v_{tot}sin(α)$
Dove la velocità totale del sistema corrisponde proprio alla velocità del centro di massa.
La conservazione della quantità di moto può anch'essa essere divisa nelle due componenti
$p_{tot_xi}=p_{tot_xf}$
$p_{tot_yi}=p_{tot_yf}$
Inizialmente la pallina 1 si muove solo sull'asse X mentre la pallina 2 solo sull'asse Y. Quindi la pallina 1 rappresenta la quantità di moto sull'asse X mentre la pallina 2 la quantità di moto sull'asse Y
$m_1v_1=p_{tot_xf}$
$m_2v_2=p_{tot_yf}$
Sostituendo le quantità di moto finali con le due componenti otteniamo
$m_1v_1=(m_1+m_2)v_{CM}\cdot cos(α)$
$m_2v_2=(m_1+m_2)v_{CM}\cdot sin(α)$
In queste equazioni l'unica quantità che viene scomposta nelle sue due componenti è la velocità totale
$v_{CM_x}=v_{CM}\cdot cos(α)$
$v_{CM_y}=v_{CM}\cdot sin(α)$
Quindi dalle due equazioni possiamo ricavare le due componenti della velocità del centro di massa
$v_{CM_x}=\frac{m_1v_1}{m_1+m_2}$
$v_{CM_y}=\frac{m_2v_2}{m_1+m_2}$
Per ricavare un vettore dalle sue componenti dobbiamo applicare il teorema di Pitagora alle due componenti
$v_{CM}=\sqrt{(\frac{m_1v_1}{m_1+m_2})^2+(\frac{m_2v_2}{m_1+m_2})^2}$
Dall'espressione che abbiamo trovato possiamo raccogliere $(m_1+m_2)^2$ e portarlo fuori dalla radice
$v_{CM}=\frac{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}{m_1+m_2}$
ANGOLO α
Dalla formula della componente X della velocità del centro di massa
$v_{CM_x}=v_{tot}cos(α)$
Possiamo sostituire $v_{CM_x}$ e $v_{CM}$ con le due espressioni che abbiamo trovato prima
$v_{CM_x}=\frac{m_1v_1}{m_1+m_2}$
$v_{CM}=\frac{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}{m_1+m_2}$
Sostituendo nell'espressione otteniamo
$\frac{m_1v_1}{m_1+m_2}=\frac{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}{m_1+m_2}cos(α)$
Da qui possiamo ricavare l'angolo α
$cos(α)=\frac{m_1v_1}{m_1+m_2}\cdot \frac{m_1+m_2}{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}$
Semplificando otteniamo
$cos(α)=\frac{m_1v_2}{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}$
E applicando l'arcocoseno ad entrambi i membri otteniamo l'angolo α
$α=arccos(\frac{m_1v_2}{\sqrt{(m_1v_1)^2+(m_2v_2)^2}})$
