Per prima cosa dobbiamo capire qual è il punto di rotazione della tavola. Siccome il gatto si trova sull'estremità destra il punto su cui la tavola ruota è il cavalletto di destra
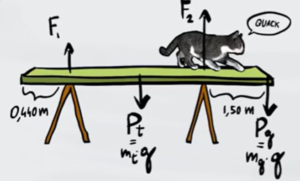
Sul cavalletto di sinistra non è presente alcune forza, quindi la forza del cavalletto $F_1$ è uguale a 0
$F_1=0$
Inoltre la forza del cavalletto di destra $F_2$ è applicata sul punto di rotazione della tavola, per cui il suo momento è nullo a causa della distanza nulla tra la forza e il punto di rotazione della tavola
$M_{F_2}=F_2\cdot 0=0$
EQUILIBRIO DEI MOMENTI
Per garantire l'equilibrio della tavola, dobbiamo scrivere l'equilibrio dei momenti:
$P_gd-m_tg=0$
Dove $P_g$ è il peso del gatto e $P_t$ il peso della tavola.
$m_ggd-m_tgd=0$
Il gatto si trova all'estremità destra della tavola, quindi la distanza tra la sua forza peso e il cavalletto di destra è $d=1,5m$ come riportato in figura
$1,5m_ggd-m_tgd=0$
Il peso della tavola è una forza che ha come direzione il centro della tavola stessa, quindi per poter ricavare la distanza dobbiamo sottrarre alla lunghezza totale della tavola $L=4m$ la distanza tra i due cavalletti e gli estremi
$d=L-0,44-1,5=1m$
Questa distanza è la distanza tra i due cavalletti, per poter trovare la distanza tra il centro e il cavalletto di destra dobbiamo dividerla per 2
$d=0,5m$
Adesso possiamo riscrivere l'equilibrio dei momenti
$1,5m_gg-0,5m_tg=0$
Da questa equazione possiamo ricavare la massa del gatto
$1,5m_gg=0,5m_tg$
$m_g=\frac{0,5m_tg}{1,5g}=2,33kg$
SECONDA DOMANDA
Nella seconda domanda viene chiesta la distanza massima a cui può arrivare il gatto prima che la tavola si ribalti. In pratica dobbiamo calcolare la distanza tra il gatto e il cavalletto di destra massima in equilibrio usando la stessa equazione che abbiamo usato per l'equilibrio dei momenti per la prima domanda
$m_ggx=0,5m_tg$
E questa volta al posto di ricavare la massa del gatto, dobbiamo ricavare la distanza incognita $x$ tra il gatto e il cavalletto di destra
$x=\frac{0,5m_tg}{m_gg}$
A questo punto possiamo semplificare al denominatore e al numeratore $g$. Sostituendo la massa del gatto con $m_g=2,8kg$ otteniamo:
$x=\frac{0,5m_t}{m_g}=1,25m$
Dai dati sappiamo che la distanza tra il cavalletto di destra e l'estremità destra è 1,5 metri, quindi per poter ricavare la distanza massima tra il gatto e l'estremità destra basta fare la differenza tra queste due distanze
$d=1,5-1,25=0,25m$
