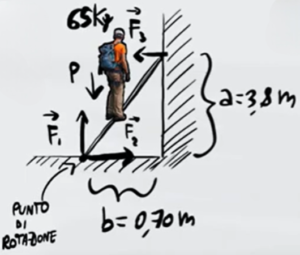
Per prima cosa dobbiamo scegliere il punto di rotazione della scala tra i due estremi. Per comodità scegliamo l'estremo basso.
La scala non sta né ruotando e né si sta muovendo, quindi sulla scala vale l'equilibrio delle forze e l'equilibrio dei momenti
EQUILIBRIO DEI MOMENTI
Come punto di rotazione abbiamo scelto l'estremo basso per cui le forze applicate su quel punto ($F_1$ e $F_2$) hanno momento nullo perché sono distanti 0 dal punto di rotazione della scala
$M_{F_1}=F_1\cdot 0=0$
$M_{F_2}=F_2\cdot 0=0$
Quindi per l'equilibrio dei momenti sono presenti solo due forze: il peso della persona $P$ e la reazione vincolare della parete sulla scala $F_3$.
Il peso spinge la scala verso il basso facendola ruotare in senso orario, la forza $F_3$ invece spinge la scala in direzione opposta in una rotazione antioraria. Siccome i due momenti sono opposti prendiamo come positivo il momento antiorario di $F_3$ e come negativo il momento orario del peso
$F_3d-Pd=0$
$F_3d-mgd=0$
Come si può vedere dall'immagine, la distanza tra la forza $F_3$ e il punto di rotazione è $a=3,8m$ mentre la distanza tra il peso e il punto di rotazione è la metà di $b$, questo perché la persona si trova a metà della scala
$F_3a-mg\frac{b}{2}=0$
Da questa equazione ricaviamo la forza $F_3$
$F_3a=mg\frac{b}{2}$
$F_3=mg\frac{b}{2a}=58,5N$
Per poter ricavare le altre incognite dobbiamo utilizzare l'equilibrio delle forze.
EQUILIBRIO DELLE FORZE
Sulla scala ci sono forze che agiscono verso l'alto o verso il basso ($F_1$ e $P$) e forze che agiscono a sinistra e a destra ($F_2$ e $F_3$), quindi l'equilibrio delle forze va diviso in due parti considerando le forze verso l'alto o il basso come asse Y e le forze a destra o a sinistra come asse X
ASSE X → $F_2-F_3=0$
ASSE Y → $F_1-mg=0$
Il meno va messo perché le forze sono opposte tra loro.
Dall'equilibrio dei momenti abbiamo ricavato la forza $F_3$ quindi possiamo ricavare anche la forza $F_2$ dall'equilibrio sull'asse X
$F_2=F_3=58,5N$
Dall'equilibrio sull'asse Y, invece, possiamo ricavare la forza $F_1$
$F_1=mg=638N$
