Per risolvere il problema dobbiamo utilizzare la conservazione del lavoro
$L=0$
Quindi la somma di energia cinetica e potenziale della persona è uguale a 0
$ΔE+ΔU=0$
ENERGIA CINETICA
L'energia cinetica totale del corpo è la differenza tra energia finale ed energia inziale
$ΔE=E_f-E_i$
Sostituendo con la formula dell'energia cinetica otteniamo:
$ΔE=\frac{1}{2}mv_{f}^2-\frac{1}{2}mv_{i}^2$
Non si hanno informazione né sulla velocità inziale della persona e né sulla velocità finale, quindi possiamo supporre che la persona sia caduta da ferma dal ponte $v_i=0$ e che alla fine della caduta si sia fermata $v_f=0$. Di conseguenza l'energia cinetica totale è uguale a 0
$ΔE=0-0=0$
ENERGIA POTENZIALE
La persona è tenuta in aria da una corda elastica. Quindi da una parte è presente energia potenziale elastica mentre dall'altra energia potenziale gravitazionale data dal peso della persona.
$ΔU_{tot}=ΔU_{peso}+ΔU_{molla}$
Usando le formule delle due energie potenziali otteniamo
$ΔU_{tot}=mgh_f-mgh_i+\frac{1}{2}kx_{f}^2-\frac{1}{2}kx_{i}^2$
L'altezza finale ed inziale sono dati nel problema e sono rispettivamente 4 metri e 30 metri. Prima del salto la corda non viene allungata per cui l'allungamento inziale è uguale a 0 $x_i=0$
$ΔU_{tot}=mgh_f-mgh_i+\frac{1}{2}kx_{f}^2$
LAVORO TOTALE
L'energia cinetica totale è uguale a 0, per cui la conservazione del lavoro è semplicemente la conservazione dell'energia potenziale
$ΔU_{tot}=0$
$mgh_f-mgh_i+\frac{1}{2}kx_{f}^2=0$
Da questa equazione possiamo ricavare la costante elastica della corda $k$.
$\frac{1}{2}kx_{f}^2=-mgh_f+mgh_i$
$k=\frac{2}{x_{f}^2}(-mgh_f+mgh_i)$
Dove l'allungamento finale $x_f$, come si può vedere dall'immagine, è semplicemente la differenza tra l'altezza iniziale e l'altezza finale
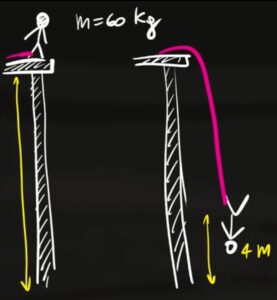
$x_f=h_i-h_f=30m-4m=26m$
Sostituendo i dati nell'equazione ricaviamo la costante elastica $k$
$k=45,28$ $N/m$
