Il moto armonico è la proiezione di un moto circolare uniformemente accelerato sul suo diametro

In pratica il moto armonico rappresenta il movimento del puntino rosso che c'è nel disegno sopra.
Questo puntino non si muove di semplice moto rettilineo ma oscilla. Cioè parte da uno dei due estremi del diametro del cerchio, accelera fino a raggiungere il centro e poi decelera fino a fermarsi all'altro estremo del diametro per poi ricominciare. Questo tipo di moto è rappresentato da un'onda.
La legge oraria del moto armonico è
$x_f=x_i+Rcos(ωt)$
Dove R è il raggio del cerchio e ω la velocità angolare, detta anche pulsazione. Facendo la derivata prima e seconda dello spostamento ricaviamo velocità e accelerazione
$v=-Rωsin(ωt)$
$a=-Rω^2cos(ωt)$
Dove l'accelerazione nel moto armonico rappresenta l'accelerazione centripeta.
Il moto armonico descrive il movimento delle molle e dei pendoli, quest'ultimi hanno due formule in particolare per le pulsazioni deòòa molla e del pendolo
$ω_{molla}=\sqrt{\frac{k}{m}}$
Dove m è la massa del corpo attaccato alla molla
$ω_{pendolo}=\sqrt{\frac{g}{L}}$
Dove L è la lunghezza del pendolo
- Esercizio 1
Ad una molla con costante elastica $k=100 N/m$ è attaccato un corpo di massa $m=50 g$. La molla viene tirata dal corpo con forza $F=80 N$. Della molla, calcola lo spostamento massimo, la velocità massima e l'accelerazione massima.
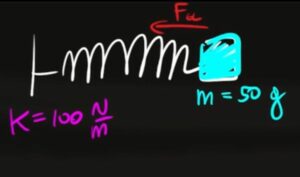
Ad una molla con costante elastica $k=100 N/m$ è attaccato un corpo di massa $m=50 g$. La molla viene tirata dal corpo con forza $F=80 N$. Calcola in quanto tempo la molla compie un'oscillazione.
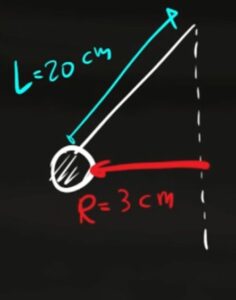
Un pendolo è lungo $L=20 cm$ con un oscillazione massima dal centro di 3 centimetri. Calcola lo spostamento, la velocità e l'accelerazione dopo 1,5 secondi.
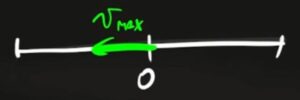
Una molla con costante elastica $k=200 N/m$ ha attaccato un corpo di massa $m=300g$. La mola viene compressa dal corpo di 12 centimetri. A che distanza dalla posizione di riposo si ha la velocità massima?
Una molla con costante elastica $k=200 N/m$ ha attaccato un corpo di massa $m=300g$. La molla viene compressa dal corpo di 12 centimetri. In che posizione si ha la velocità di oscillazione della molla uguale a 1/4 della velocità massima?
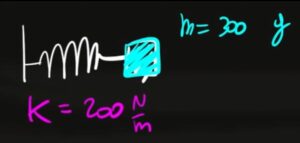
Una molla con costante elastica $k=200 N/m$ ha attaccato un corpo di massa $m=300g$. La mola viene compressa dal corpo di 12 centimetri. Calcola l'accelerazione massima della molla
