Per risolvere questo problema dobbiamo utilizzare il concetto della parabola di sicurezza. La parabola di sicurezza si riferisce alla traiettoria ideale di un corpo che, dopo essere lanciato, segue una curva che garantisce che il corpo atterri in una zona precisa.
In questo caso il corpo è il pallone e la zona precisa è il piano inclinato.
La parabola di sicurezza è una parabola di equazione:
$y=\frac{v^2}{2g}-\frac{g}{2v^2}x^2$
Questa equazione ci serve per trovare i punti di intersezione della parabola con il piano inclinato. Il piano inclinato è un triangolo rettangolo, quindi l'equazione della retta che lo descrive è quella di un retta dove Y è l'altezza e X la base del triangolo.
$y=mx$
Dalla trigonometria sul triangolo rettangolo sappiamo che l'altezza è uguale alla base moltiplicata per la tangente dell'angolo
$y=tan(30°)x$
La gittata massima sarà dunque il punto X in cui il pallone tocca il piano. Cioè dobbiamo ricavare il punto X in cui la parabola e la retta si intersecano
$\frac{v^2}{2g}-\frac{g}{2v^2}x^2=tan(30°)x$
Il risultato è un equazione di secondo grado, per risolverla dobbiamo riordinare i termini portandoli tutti a sinistra dell'uguale
$-\frac{g}{2v^2}x^2-tan(30°)x+\frac{v^2}{2g}$
Per semplificare l'equazione calcoliamo i termini che moltiplicano le $x$
$-0,0078x^2-0,577x+31,888=0$
Utilizzando la formula risolutiva delle equazioni di secondo grado otteniamo:
$x=\frac{0,577\pm \sqrt{(-0,577)^2-4(-0,0078)(31,888)}}{-2\cdot 0,0078}$
I due risultati sono
$x_1=36,82 m$
$x_2=-110,46 m$
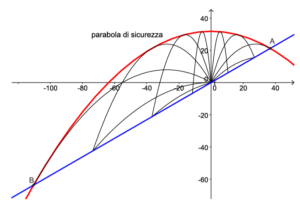
Sul grafico il punto A si riferisce alla gittata sul piano inclinato in salita mentre il punto B alla gittata in discesa dal piano inclinato. Il punto A, siccome indica una salita, deve essere positivo quindi è il punto $x_1=36,82 m$ mentre il punto B è in discesa per cui è negativo e descritto da $x_2=-110,46 m$
