Per prima cosa rappresentiamo sul piano cartesiano il moto parabolico del pallone
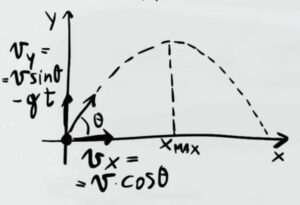
Intanto ci scriviamo le formule per le due componenti:
$v_y=vsin(θ)$
$v_x=vcos(θ)$
Sul grafico il punto $x_{max}$ rappresenta il punto sull'asse X in cui l'altezza della parabola è massima. Dalle equazioni del moto rettilineo
$v=\frac{x}{t}$
Sul piano orizzontale la velocità è $v_x$ mentre come spazio percorso possiamo scegliere $x_{max}$. Per raggiungere il punto di massima altezza la palla ci impiega un tempo detto tempo di salita. Il tempo di salita è un dato che abbiamo dal problema e che vale 0,75 secondi.
$v_x=\frac{x_{max}}{t_{salita}}$
Da questa equazione possiamo ricavare il punto di massima altezza
$x_{max}=v_xt_{salita}$
Come si può vedere dal grafico, il punto X di altezza massima si trova precisamente a metà percorso orizzontale. Lo spazio totale percorso orizzontalmente è la gittata.
Quindi il punto X di altezza massima si trova a metà gittata
$x_{max}=\frac{G}{2}$
La formula della gittata si può ricavare calcolando il vertice x della parabola ed è:
$G=\frac{2v_xv_y}{g}$
Dividendo la gittata per 2 otteniamo $x_{max}$
$x_{max}=\frac{v_xv_y}{g}$
$x_{max}$ la possiamo sostituire con la formula del moto
$v_xt_{salita}=\frac{v_xv_y}{g}$
Dividiamo entrambi i lati dell'equazione per $v_x$ ottenendo
$t_{salita}=\frac{v_y}{g}$
Da questa equazione dobbiamo ricavare l'angolo θ, quindi dobbiamo sostituire $v_y$ con la formula della componente
$t_{salita}=\frac{vsin(θ)}{g}$
Da questa equazione ricaviamo $sin(θ)$
$sin(θ)=\frac{gt_{salita}}{v}$
Per ricavare l'angolo θ basta applicare ad entrambi i membri la funzione inversa del seno
$θ=arcsin(\frac{gt_{salita}}{v})=46,2°$
