Prodotto scalare e vettoriale – esercizi svolti

Clicca qui per vedere la pagina degli esercizi sul prodotto scalare e vettoriale

• Esercizio 1
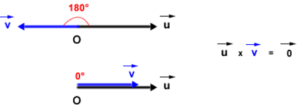
  Nell'esercizio non è indicato l'angolo di inclinazione dei due vettori, quindi lo poniamo uguale a 0

  $ ß=0 $

  Ora facciamo il prodotto dei due moduli per il coseno dell'angolo ß

  $ \vec{A}\cdot \vec{B}=|A|\cdot |B|\cdot cos(ß)=3\cdot 4 \cdot 1 =12 $

• Esercizio 2
  In questo esercizio sono date le componenti x e y dei due vettori, quindi per trovare i moduli basta usare il teorema di Pitagora

  $ |u|=\sqrt{3^2+(-2)^2}=\sqrt{13} $

  $ |v|=\sqrt{4^2+0^2}=4 $

  Ora possiamo fare il prodotto dei due moduli per il coseno dell'angolo

  $ \vec{u}\cdot \vec{v}=|u|\cdot |v|\cdot cos(45°)=10,2 $

• Esercizio 3
  Stessa cosa dell'esercizio 2, dobbiamo ricavare il modulo dei due vettori dalle loro componenti usando il teorema di Pitagora

 

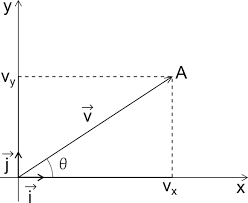
$ |A|=\sqrt{3^2+4^2}=5 $

$ |B|=\sqrt{1^2+2^2}=\sqrt{5} $

Per il prodotto vettoriale, facciamo il prodotto dei moduli per il seno dell'angolo. Siccome nell'esercizio non viene dato l'angolo lo poniamo uguale a 0

$ |\vec{A}×\vec{B}|=|A|\cdot |B|\cdot sin(0°)=0 $

Il prodotto si annulla perché il seno di 0° è 0.

• Esercizio 4
  Calcoliamo i moduli dei due vettori usando il teorema di Pitagora

  $ |u|=\sqrt{5^2+(-3)^2}=\sqrt{34} $

  $ |v|=\sqrt{2^2+4^2}=\sqrt{20}=2\sqrt{5} $

  Ora facciamo il prodotto dei due moduli per il seno di 60°

  $ |\vec{u}×\vec{v}|=|u|\cdot |v|\cdot sin(60°)=22,6 $

• Esercizio 5
  Nell'esercizio vengono già date le componenti dei due vettori

  $ p_x=-1, p_y=2, p_z=3 $

  $ q_x=2, q_y=-1, q_z=4 $

  Quindi possiamo calcolare il prodotto vettoriale facendo il determinante del prodotto dei due vettori rappresentati sotto forma di matrici (mostrato nella pagina di teoria). Il risultato è questa formula:

  $\vec{p}×\vec{q}=(q_yp_z-q_zp_y)x+(q_zp_x-q_xp_z)y$

  $+(q_xp_y-q_yp_x)z$

  Svolgendo i calcoli troviamo l'equazione del vettore risultante

  $ \vec{C}=-11x-10y+3z $

  Le componenti del vettore C sono i coefficenti di x,y e z

  $ \vec{C}=(-11,-10,3) $

  In questo modo abbiamo ricavato la direzione del vettore.
  Il modulo del vettore C, invece, si calcola tramite il teorema di pitagora in 3 dimensioni delle sue compoenenti

  $ |C|=\sqrt{(-11)^2+(-10)^2+3^2}=\sqrt{230} $

Per ricavare il verso del vettore dobbiamo calcolare il vettore unitario, cioè il vettore di lunghezza 1 che ha la stessa direzione del vettore C e si calcola in questo modo:

$ \hat{C}=\frac{\vec{C}}{|C|} $

Questo va separato nelle tre componenti di C

$ \hat{C}=(\frac{C_x}{|C|}, \frac{C_y}{|C|}, \frac{C_z}{|C|})=(-\frac{11}{\sqrt{230}}, -\frac{10}{\sqrt{230}}, \frac{3}{\sqrt{230}}) $

Il verso del vettore unitario è indicato dal verso in cui queste componenti puntano, cioè lungo il cammino positivo dei valori dati.

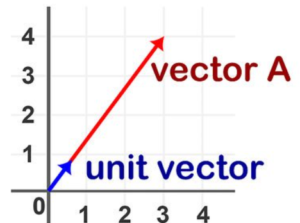
Rappresentazione grafica del vettore unitario in 2 dimensioni