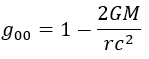Approssimazioni della relatività generale

Per dei corpi molto massicci il tensore metrico si può approssimare alla somma di un tensore di curvatura h e il tensore di spazio-tempo piatto.

 

Partendo dal principio di equivalenza

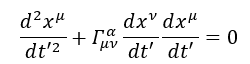
Per arrivare all’obiettivo finale (trovare le equazioni di campo) prendiamo solamente la componente temporale (componente 0) dei vari indici μv

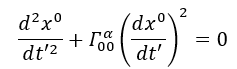
Però noi abbiamo che x₀ =ct

Dalla connessione affine ricavata in tensore metrico e connessione affine abbiamo che

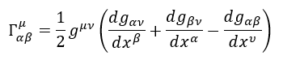
E usando le approssimazioni mostrate in precedenza otteniamo il seguente risultato (trascurando anche altri termini)

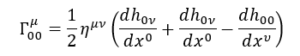
Ponendo uguale a 0 i primi due termini dentro la parentesi otteniamo

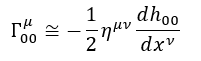
In questo modo otteniamo un nuovo principio di equivalenza ponendo tutte le x come dei vettori

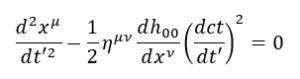
Ora poniamo gli indici dei termini uguali a i (cioè includiamo tutte le componenti tranne quelle temporali) ottenendo  (perché è l’unico caso in cui  non è uguale a 0) e il resto diventano delle quantità vettoriali

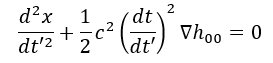
Il primo termine lo possiamo scrivere in questo modo:

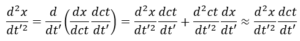
Ottenendo

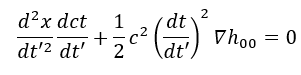
Quindi

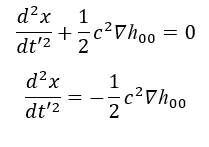
Dalla gravità di Newton sappiamo che

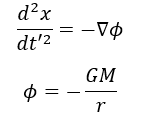
Quindi dalla prima equazione otteniamo il potenziale gravitazionale i  relatività generale

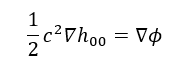
Integrando ambo i membri otteniamo

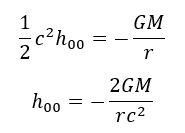
Dalle approssimazioni mostrate in precedenza possiamo affermare che

Quindi