Inoltre il principio di equivalenza predice l’esistenza di una quarta dimensione in cui compare anche il tempo.
Tutto parte considerando la conservazione del quadrimpulso (quantità di moto quadridimensionale)
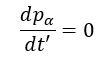
In cui t’ è il tempo proprio, cioè quello che misura il corpo stesso.
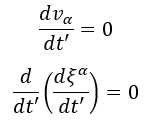
Siccome la quantità di moto è mv (in cui v è la velocità quadridimensionale) possiamo riscrivere la quantità di moto dell’equazione ponendo la massa diversa da 0, ottenendo
εa è una coordinata nello spazio non inerziale (soggetto ad una accelerazione data dalla gravità) che si può scrivere come funzione di una xμ nello spazio inerziale (in quiete o in moto rettilineo uniforme) in questo modo:
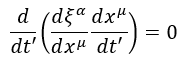
Dopo procediamo facendo la derivata tramite la regola del prodotta di funzioni
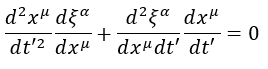
La derivata seconda della εa si può scrivere come il prodotto di due derivate che diano come risultato la derivata seconda di partenza (è solamente un metodo per riscrivere meglio la derivata seconda nel tempo e nello spazio)
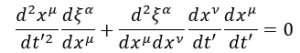
Moltiplichiamo ambo i membri dell’equazione per una nuova derivata di una coordinata inerziale in una coordinata non inerziale

In questo modo abbiamo che nel primo termine il prodotto con
![]()
Per semplificare l’equazione poniamo una connessione affine (cioè un collegamento tra coordinate di un sistema non inerziale e coordinate di un sistema inerziale)
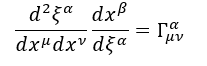
In modo tale da ottenere il principio di equivalenza
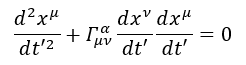
In questa ultima equazione possiamo vedere che il primo termine è una coordinata inerziale, cioè in assenza di gravità, mentre il secondo termine indica proprio la presenza di gravità che modifica le coordinate del corpo.
