Il concetto di conservazione nella fisica
Nel percorso di studi di fisica in un liceo scientifico, molte delle formule e delle leggi descritte si fondano su un concetto cardine: la conservazione o l'invarianza di alcune quantità nel tempo. Questo principio appare quasi ovvio per noi esseri umani, soprattutto in relazione alla conservazione della materia: come potrebbe qualcosa crearsi dal nulla? E, d'altro canto, come e perché dovrebbe sparire nel nulla?
Le radici filosofiche della conservazione
Queste domande hanno radici filosofiche antiche che risalgono a Parmenide di Elea, filosofo greco vissuto tra il VI e il V secolo a.C., il quale sosteneva che "ciò che è, è e non può non essere; ciò che non è, non è e non può essere". Tale principio fu poi ripreso come fondamento della fisica epicurea e si tradusse nella celebre locuzione lucreziana "ex nihilo nihil fit", cioè "dal nulla non può nascere nulla". Nel suo De rerum natura, il poeta latino Lucrezio fornì molti esempi assurdi per convincere della veridicità di questo principio, come "gli uomini potrebbero nascere dal mare, i pesci dal cielo". Nel corso della storia del pensiero, questa proposizione si è trasformata nella famosa frase "nulla si crea, nulla si distrugge, ma tutto si trasforma", attribuita al chimico Antoine Lavoisier e alla sua legge di conservazione della massa.
La rivoluzione einsteiniana
Per secoli, se non millenni, si è pensato che queste leggi di conservazione fossero fondamentali e intrinseche nella struttura stessa dell'universo: erano i postulati del cosmo. Tuttavia, un certo fisico tedesco, che già nel 1905 aveva rivoluzionato 2300 anni di fisica con la sua "teoria della relatività ristretta", dieci anni più tardi, con la sua "teoria della relatività generale", dimostrò che l'energia non viene conservata in ogni caso. Così Albert Einstein demolì nuovamente i principi su cui si reggeva la fisica classica, come se fossero foglie d'autunno.
Per comprendere la contraddizione che emerge dalla teoria di Einstein è necessario breve excursus sulla storia dell’ottica: Christiaan Huygens nel 1690 pubblicò la sua teoria ondulatoria della luce, secondo cui questa era un’onda trasversale che si propagava in tutte le direzioni attraverso un mezzo chiamato “etere luminifero” che permeava l’intero cosmo; Isaac Newton pubblicò nel 1704 la sua teoria corpuscolare della luce, sostenendo che questa si comportasse come un fascio di corpuscoli, in seguito chiamati “fotoni” (dal greco, φος, luce). La teoria di Huygens fu rifiutata in favore di quella di Newton, che forniva una spiegazione a tutti i fenomeni allora conosciuti: tuttavia, riemerse nel 1821 con i lavori di Fresnel e Poisson per poi affermarsi completamente nel 1850.
Fu ulteriormente confermata dall’elettromagnetismo di Maxwell, che dimostrava la natura elettromagnetica della luce. Un mistero rimaneva però irrisolto: provare l’esistenza dell’”etere luminifero”, che sfuggiva a ogni misurazione. Max Planck nel 1900, per risolvere il problema della radiazione di corpo nero, teorizzò che, nonostante la luce fosse un’onda, l’energia che poteva perdere o guadagnare era “quantizzata”, cioè multipla intera di una costante fondamentale, e proporzionale alla sua frequenza. Infine Einstein nel 1905 utilizzò un’ eventuale duale natura della luce, sia onda che corpuscolo, per spiegare l’effetto fotoelettrico, dando inizio alla fisica moderna.

L'espansione dell'universo e la perdita di energia
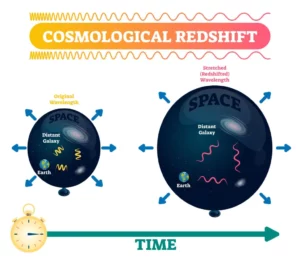
La teoria della relatività generale di Einstein presuppone che la luce si muova a velocità costante attraverso l'universo, ma poiché questo è in espansione, l'onda di luce viene "allungata" (poiché la sorgente si allontana dal ricevitore), aumentando così la lunghezza d'onda e diminuendo la frequenza. Tuttavia, secondo la relazione di Planck, l'energia di quest'onda diminuisce anch'essa e "sparisce", poiché non viene emessa in nessun altro modo, contraddicendo la legge di conservazione dell'energia dell'universo.
Il contributo di Emmy Noether
All'epoca, questo fatto suscitò grande clamore nella comunità scientifica. I matematici David Hilbert e Felix Klein chiesero aiuto a una giovane matematica, Emmy Noether, per cercare di risolvere questo paradosso. Non solo riuscì a comprendere perché la teoria di Einstein annullava la legge di conservazione in alcuni casi, ma dimostrò che tutte le leggi di tipo analogo non sono fondamentali, ma derivano da un teorema ancora più strutturale, oggi noto come Teorema di Noether. Esso può essere enunciato come segue: "Se un sistema presenta una simmetria continua, allora esistono delle quantità corrispondenti che si conservano nel tempo".
Applicazioni del Teorema di Noether
Ad esempio, alla simmetria di traslazione corrisponde la conservazione del momento lineare (o quantità di moto); alla simmetria rotazionale, quella del momento angolare; alla simmetria temporale, quella dell'energia. Questo teorema si applica principalmente alla meccanica, ma è stato anche esteso alla teoria dei campi, di cui costituisce la base. Ha anche permesso di scoprire nuovi tipi di grandezze fisiche: se una teoria matematica presenta una determinata simmetria, allora deve esistere una quantità fisica che non cambia, come nel caso della "carica colore" all'interno dei quark.
I contributi di Emmy Noether alla matematica
Emmy Noether ha avuto un impatto così profondo in ambito matematico che il suo lavoro è diviso in tre periodi principali. Nel primo (1908-1919), contribuì in modo significativo alle teorie dei campi numerici e il suo teorema è considerato uno dei più importanti mai dimostrati nello sviluppo della fisica moderna. Nel secondo periodo (1920-1926), iniziò a sviluppare la teoria degli ideali e a "cambiare la faccia dell'algebra astratta", tanto che alcuni oggetti matematici sono chiamati Noetheriani in suo onore. Nel terzo periodo (1927-1935), pubblicò lavori sulle algebre non commutative e sull'unificazione della teoria rappresentativa dei gruppi con la teoria degli ideali.
La vita di Emmy Noether
Nata il 23 marzo 1882 dal matematico Max Noether, Amalie Emmy Noether mostrò fin da piccola un acume eccezionale, risolvendo un rompicapo a una festa per bambini. Tuttavia, come molte ragazze del suo tempo, le furono insegnati compiti domestici come cucinare, pulire e suonare il pianoforte, attività che non la interessavano. Nonostante fosse fluente in francese e inglese, doti che le avrebbero permesso di insegnare nelle scuole per ragazze, decise di continuare gli studi universitari a Erlangen, una scelta non convenzionale per una donna dell'epoca. Fu una delle due uniche donne tra 986 studenti e poté partecipare alle lezioni solo come uditrice, con il permesso specifico dei professori. Nonostante questi ostacoli, superò l'esame di laurea a Norimberga e nel semestre invernale 1903-1904 studiò a Gottinga, assistendo alle lezioni di Schwarzschild, Minkowski, Klein e Hilbert. Col tempo, le restrizioni sulla partecipazione delle donne alle lezioni furono abolite in quell'università.
Le difficoltà nel mondo accademico
Tornata a Erlangen, Emmy dichiarò di voler perseguire esclusivamente gli studi matematici, e con la sua dissertazione del 1907 ottenne il dottorato. Fino al 1915, insegnò lì senza retribuzione, spesso sostituendo suo padre malato. Nella primavera di quell'anno, fu invitata da Hilbert e Klein a tornare a Gottinga, ma incontrarono l'opposizione dei filologi e degli storici della facoltà di filosofia, che insistevano che una donna non avrebbe dovuto diventare privatdozent (docente a tempo pieno). "Che diranno i nostri soldati quando torneranno all'università e vedranno di dover imparare ai piedi di una donna?" disse uno degli oppositori. Hilbert rispose indignato: "Non vedo come il sesso del candidato possa essere un argomento contrario alla sua ammissione come privatdozent. Dopo tutto, siamo in un'università, non in una sorgente termale."
Il riconoscimento tardivo e l'impatto internazionale
Nei primi anni di insegnamento, Emmy Noether non aveva né una posizione ufficiale né uno stipendio. Le sue lezioni erano spesso pubblicizzate sotto il nome di Hilbert, come se fosse sua assistente. Tuttavia, con la dimostrazione del suo teorema, le fu riconosciuto un certo merito anche all'estero, tanto che la sua scoperta in campo fisico fu paragonata al teorema di Pitagora nella geometria euclidea. Dopo la fine della Prima Guerra Mondiale, grazie alla rivoluzione del 1919, le donne ottennero maggiori diritti e l'università le concesse l'abilitazione all'insegnamento nello stesso giugno. Tre anni dopo, ricevette dal ministro dell'educazione prussiano una lettera che le conferiva il titolo di professoressa associata. Tuttavia, nonostante questo riconoscimento, non le venne assegnato alcun salario. Solo l'anno successivo, come insegnante di algebra, iniziò a ricevere una retribuzione.
Gli ultimi anni e il legato di Emmy Noether
Fino al 1933, Emmy Noether era ben vista nell'ambito accademico sia per la sua brillantezza che per il suo carattere altruista: molti matematici dell'epoca la citavano nei loro lavori per la sua generosità di idee, anche in campi che non aveva mai studiato direttamente. Con l'ascesa di Hitler e l'introduzione delle leggi razziali, fu espulsa dall'università a causa delle sue origini ebraiche. Grazie all'aiuto di Einstein e Weyl, trovò rifugio a Princeton, per poi insegnare al Bryn Mawr College.
Nell'aprile del 1935, le fu diagnosticato un tumore al bacino e, durante l'operazione di rimozione, i medici scoprirono una cisti ovarica che le causò un collasso circolatorio, portandola alla morte.

Conclusione: Il modello di Emmy Noether
Oggi, Emmy Noether è considerata una delle menti più brillanti del XX secolo e la più grande matematica della storia. La sua vita non fu facile, essendo una figura anticonformista e controcorrente: una donna, ebrea, molto più brillante della maggior parte degli uomini che allora detenevano il potere, che perseguì studi scientifici fino a ottenere una cattedra in uno dei campi più astratti della matematica. È un modello da seguire non solo per i suoi straordinari risultati accademici, ma anche per la sua tenacia nel combattere contro gli stereotipi e la società che cercava di ostacolarla nel raggiungimento dei suoi sogni, prima per il suo genere e poi per la religione che professava.
Con l'aiuto di lorenzo Montano









katana